Distribución De Muestreo ( De la proporcion y la Varianza)

Distribución De Muestreo De La Proporción

Existen ocasiones en las cuales no estamos interesados en la media de la muestra, sino que queremos investigar la proporción de artículos defectuosos o la proporción de alumnos reprobados en la muestra. La distribución muestral de proporciones es la adecuada para dar respuesta a estas situaciones. Esta distribución se genera de igual manera que la distribución muestral de medias, a excepción de que al extraer las muestras de la población se calcula el estadístico proporción (p=x/n en donde "x" es el número de éxitos u observaciones de interés y "n" el tamaño de la muestra) en lugar del estadístico media.

Parámetros de una distribución muestral de una proporción.

Ejemplo:

Una fábrica de pasteles fabrica, en su producción habitual, un  de pasteles defectuosos. Un cliente recibe un pedido de  pasteles de la fábrica. Calcula la probabilidad de que encuentre más del  de pasteles defectuosos.

Estamos tomando una muestra de tamaño , de una población donde la proporción de pasteles defectuosos es de . Podemos usar las Distribución Muestral de Proporciones, que se ajusta a una normal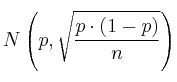 

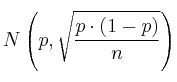
En nuestro ejemplo, si sustituimos los valores de 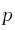 y 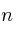 y calculamos, sería 

 a) 

Se ha tipificado la variable y se ha hecho uso de la tabla de la N(0,1)

Distribución De Muestreo De La varianza

Ejemplo de aplicación :

Estimación por intervalos

La estimación por intervalos consiste en establecer el intervalo de valores donde es más probable se encuentre el parámetro. La obtención del intervalo se basa en las siguientes consideraciones:

a) Si conocemos la distribución muestral del estimador podemos obtener las probabilidades de ocurrencia de los estadísticos muestrales.

b) Si conociéramos el valor del parámetro poblacional, podríamos establecer la probabilidad de que el estimador se halle dentro de los intervalos de la distribución muestral.

c) El problema es que el parámetro poblacional es desconocido, y por ello el intervalo se establece alrededor del estimador. Si repetimos el muestreo un gran número de veces y definimos un intervalo alrededor de cada valor del estadístico muestral, el parámetro se sitúa dentro de cada intervalo en un porcentaje conocido de ocasiones. Este intervalo es denominado "intervalo de confianza".

Ejemplo:

Se generan 100000 muestras aleatorias (n=25) de una población que sigue la distribución Normal, y resulta:

                        


La distribución de las Medias muestrales aproxima al modelo Normal:

                                                   

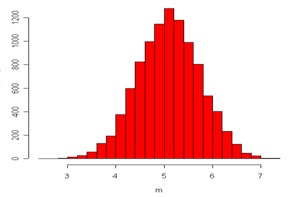
En consecuencia, el intervalo dentro del cual se halla el 95% de las Medias muestrales es:

                                                     

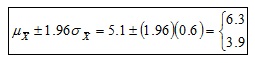
Intervalos de confianza para la media 

En este tema es sumamente importante conocer un estimación correcta de estos intervalos por lo que el presente vídeo nos guiara de la mejor manera.