Miércoles 07 de diciembre del 2016
Eventos Independientes:
Algunas situaciones de probabilidad implican más de un evento. Cuando los eventos no se afectan entre sí, se les conoce como eventos independientes. Los eventos independientes pueden incluir la repetición de una acción como lanzar un dado más de una vez, o usar dos elementos aleatorios diferentes, como lanzar una moneda y girar una ruleta. Muchas otras situaciones también pueden incluir eventos independientes. Para calcular correctamente las probabilidades, necesitamos saber si un evento influye en el resultado de otros eventos.
La principal característica de una situación con eventos independientes es que el estado original de la situación no cambia cuando ocurre un evento. Existen dos maneras de que esto suceda:
Los eventos independientes ocurren ya sea cuando:
· el proceso que genera el elemento aleatorio no elimina ningún posible resultado o
· el proceso que sí elimina un posible resultado, pero el resultado es sustituido antes de que suceda una segunda acción. (A esto se le llama sacar un reemplazo.)
Cuando A y B son dos eventos con probabilidades positivas, hemos visto que en general la probabilidad condicional del evento B dado el evento A es diferente de la probabilidad del evento B. Sin embargo, cuando se tiene la igualdad: P(B/A) = P(B) es de especial importancia porque esto quiere decir que el evento B no depende o es independiente del evento A. Es decir, no importa si ocurrió o no el evento A puesto que la ocurrencia o no de A no afecta al evento B.
Proposición 3.6: Si B es independiente de A, entonces A es independiente de B.
Demostración: De la definición de probabilidad condicional se tiene
Despejando
Como B es independiente de A, se tiene: P(B/A) = P(B) y sustituyendo en [3.3] nos conduce a la expresión
Por lo tanto
Proposición 3.7: A y B son independientes si y sólo si
Demostración: Si A y B son independientes, entonces
P(B/A) = P(B) y P(A/B) = P(A) [3.4]
De la definición de probabilidad condicional se derivó la ecuación [3.5]
[3.5]
Sustituyendo [3.4] en [3.5] se tiene:
Por otra parte, si
y
De donde A es independiente de B y B es independiente de A.
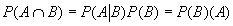
0 comentarios:
Publicar un comentario