Distribución De Muestreo

Distribución De Muestreo

Conceptos básicos Para introducir los conceptos básicos consideremos el siguiente ejemplo: Supongamos que estamos interesados en determinar el número medio de televisores por hogar en la ciudad de Caracas. Para ello consideraremos primeramente:
 Población: Conjunto de personas u objetos de interés en una Investigación. Ej: Todos los hogares de la ciudad de Caracas
 Muestra: Es una porción representativa de elementos de una población, elegida para su examen o medición directa. Note que generalmente es costoso el análisis de todos los datos, así que se hace necesario realizar las mediciones de interés sólo en una porción representativa de la población e inferir de ella resultados que corresponden a la población entera. Ej: Medir la cantidad de televisores en un grupo de hogares de varias localidades, municipios de la ciudad de Caracas, escogidos aleatoriamente de manera conveniente.
Parámetro: Es cualquier característica de una población, como la media de la población, la desviación de la población, etc. Ej: Número promedio de televisores por hogar en toda la ciudad de Caracas.
Estadístico: Es cualquier característica de una muestra, como la media de la muestra, la desviación de la muestra, etc. Ej: Número promedio de televisores calculado sólo a partir de los hogares que fueron seleccionados en la muestra.
Muestreo: Proceso de selección de muestras, se utiliza cuando no es posible contar o medir todos los elementos de la población objeto de estudio.

Distribución de muestra de la media 

Si tenemos una muestra aleatoria de una población N(m,s ), se sabe (Teorema del límite central) que la fdp de la media muestral es también normal con media m y varianza s2/n. Esto es exacto  para poblaciones normales y aproximado (buena aproximación con n>30) para poblaciones cualesquiera. Es decir es el error típico, o error estándar de la media. ¿Cómo usamos esto en nuestro problema de estimación?  Principal problema: No hay tablas para cualquier normal, sólo para la normal m=0 y s=1 (la llamada z) pero haciendo la transformación (llamada tipificación) 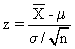                                                               una normal de media m y desviación s se transforma en z.                                                      Teorema del limite central Si una población tiene media μ y desviación típica σ, y tomamos muestras  de tamaño n (n > 30, ó cualquier tamaño si la población es "normal") las medias de estas muestras siguen aproximadamente la distribución: Consecuencias 1.Permite averiguar la probabilidad de que la media de una  muestra concreta esté en un cierto intervalo. 2.Permite calcular la probabilidad de que la suma de los  elementos de una muestra esté, a priori, en un cierto intervalo. 3.Inferir la media de la población a partir de una muestra.       Ejemplo de aplicación del teorema del limite central Las bolsas de sal envasadas por una máquina tienen μ = 500 g σ = 35 g. Las bolsas se empaquetaron en cajas de 100 unidades. 1.Calcular la probabilidad de que la media de los pesos de las  bolsas de un paquete sea menor que 495 g.