Viernes 11 de noviembre del 2016
Medidas de Centralización
Medidas de Centralización
Nos dan un centro de la distribución de frecuencias, es un valor que se puede tomar como representativo de todos los datos. Hay diferentes modos para definir el "centro" de las observaciones en un conjunto de datos. Por orden de importancia, son:
MEDIA : (media aritmética o simplemente media). es el promedio aritmético de las observaciones, es decir, el cociente entre la suma de todos los datos y el numero de ellos. Si xi es el valor de la variable y ni su frecuencia, tenemos que:
Si los datos están agrupados utilizamos las marcas de clase, es decir ci en vez de xi.
MEDIANA (Me):es el valor que separa por la mitad las observaciones ordenadas de menor a mayor, de tal forma que el 50% de estas son menores que la mediana y el otro 50% son mayores. Si el número de datos es impar la mediana será el valor central, si es par tomaremos como mediana la media aritmética de los dos valores centrales.
MODA (M0): es el valor de la variable que más veces se repite, es decir, aquella cuya frecuencia absoluta es mayor. No tiene porque ser única.
Medidas de Dispersión
Las medidas de tendencia central tienen como objetivo el sintetizar los datos en un valor representativo, las medidas de dispersión nos dicen hasta que punto estas medidas de tendencia central son representativas como síntesis de la información. Las medidas de dispersión cuantifican la separación, la dispersión, la variabilidad de los valores de la distribución respecto al valor central. Distinguimos entre medidas de dispersión absolutas, que no son comparables entre diferentes muestras y las relativas que nos permitirán comparar varias muestras.
MEDIDAS DE DISPERSIÓN ABSOLUTAS
VARIANZA ( s^2 ): es el promedio del cuadrado de las distancias entre cada observación y la media aritmética del conjunto de observaciones.
Haciendo operaciones en la fórmula anterior obtenemos otra fórmula para calcular la varianza:
Si los datos están agrupados utilizamos las marcas de clase en lugar de Xi.
DESVIACIÓN TÍPICA (s): La varianza viene dada por las mismas unidades que la variable pero al cuadrado, para evitar este problema podemos usar como medida de dispersión la desviación típica que se define como la raíz cuadrada positiva de la varianza
Para estimar la desviación típica de una población a partir de los datos de una muestra se utiliza la fórmula (cuasi desviación típica):
RECORRIDO O RANGO MUESTRAL (Re). Es la diferencia entre el valor de las observaciones mayor y el menor. Re = xmax - xmin
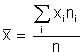





















0 comentarios:
Publicar un comentario