Distribución Hipergeometrica
Este modelo presenta similitudes con el Binomial, pero sin la suposición de independencia de éste último.
- Partimos de un conjunto formado por N individuos divididos en dos categorías mutuamente excluyentes: A y Ac; de manera que N1 individuos pertenecen a la categoría A y N2 individuos, a la categoría Ac. Por tanto, se cumple que
N = N1 + N2
- Si del conjunto anterior extraemos n individuos sin reemplazamiento (n ≤ N), la variable X que representa el número k de individuos que pertenecen a la categoría A (de los n extraídos) tiene por función de densidad:
Media y Varianza
Ejemplo:
En Una oficina donde se ensamblan computadoras, en una mesa hay 20 chips de los cuales 6 están malogrados. Primero llega el Sr. Gates y recoge 8 chips y más tarde llega el Sr. Apple y se lleva los restantes. Halle la probabilidad que solamente uno de ellos se haya llevado todos los chips defectuosos.
Distribución Binomial Negativa
Esta distribución puede considerarse como una extensión o ampliación de la distribución geométrica . La distribución binomial negativa es un modelo adecuado para tratar aquellos procesos en los que se repite un determinado ensayo o prueba hasta conseguir un número determinado de resultados favorables (por vez primera) .Es por tanto de gran utilidad para aquellos muestreos que procedan de esta manera. Si el número de resultados favorables buscados fuera 1 estaríamos en el caso de la distribución geométrica . Está implicada también la existencia de una dicotomía de resultados posibles en cada prueba y la independencia de cada prueba o ensayo, o la reposición de los individuos muestreados.
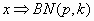
k
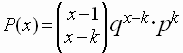
Media y Varianza
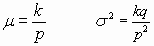
Ejemplo:
En una caja hay 8 canicas rojas, 10 verdes, 5 negras, si extraemos 6 canicas rojas al azar ¿Calcular probabilidad de que ya hayan salido 2 canicas verdes ?
p = 8 / 13 = 0.347826
q = 15 / 23 = 0.6521739
k = 6
x = 2




















0 comentarios:
Publicar un comentario