Distribución de probabilidades continuas (Distribución exponencial)

Distribución exponencial

  A pesar de la sencillez analítica de sus funciones de definición, la distribución exponencial tiene una gran utilidad práctica ya que podemos considerarla como un modelo adecuado para la distribución de probabilidad del tiempo de espera entre dos hechos que sigan un proceso de Poisson. De hecho la distribución exponencial puede derivarse de un proceso experimental de Poisson con las mismas características que las que enunciábamos al estudiar la distribución de Poisson, pero tomando como variable aleatoria , en este caso, el tiempo que tarda en producirse un hecho

Obviamente, entonces , la variable aleatoria será continua. Por otro lado existe una relación entre el parámetro a de la distribución exponencial , que más tarde aparecerá , y el parámetro de intensidad del proceso l , esta relación es a = l

Al ser un modelo adecuado para estas situaciones tiene una gran utilidad en los siguientes casos:

· Distribución del tiempo de espera entre sucesos de un proceso de Poisson

· Distribución del tiempo que transcurre hasta que se produce un fallo, si se cumple la condición que la probabilidad de producirse un fallo en un instante no depende del tiempo transcurrido .Aplicaciones en fiabilidad y teoría de la supervivencia.

   A pesar de lo dicho sobre que la distribución exponencial puede derivarse de un proceso de Poisson , vamos a definirla a partir de la especificación de su función. de densidad:

    Dada una variable aleatoria X que tome valores reales no negativos {x ³ 0} diremos que tiene una distribución exponencial de parámetro a con a ³ 0, si y sólo si su función de densidad tiene la expresión: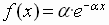 

                                                           Diremos entonces que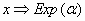 

Gráficamente como ejemplo planteamos el modelo con parámetro a =0,05

 Entonces obtenemos:

                                             

Gráficamente, la función de distribución para un modelo exponencial de parámetro a =0,05 sería :

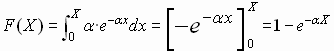
  Media y Varianza

Ejemplo de aplicación:

Relación de la distribución Exponencial y Poisson

Para un proceso de Poisson, llega a ocurrir al azar independiente del pasado, pero con un conocido del promedio a largo plazo de la tasa de 

λ$\lambda$ de éxitos por unidad de tiempo. La distribución de Poisson nos permitirá encontrar la probabilidad de obtener un determinado número de golpes.

Ahora, en lugar de fijarse en el número de visitas, nos fijamos en la variable aleatoria L(de por Vida), el tiempo que tiene que esperar para el primer golpe.

La probabilidad de que el tiempo de espera es de más de un determinado valor de tiempo es  P(L>t)=P(no hits in time t)=Λ0e−Λ0!=e−λt

P(L≤t)=1−e−λt

(la función de distribución acumulativa). Podemos obtener la función de densidad tomando la derivada de esto:
 

Nota

Cualquier variable aleatoria que tiene una función de densidad, como se dice que esta es exponencialmente distribuidos.